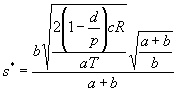四、模糊生產批量的隸屬函數與總成本函數

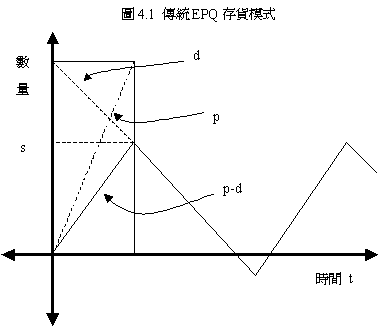
傳統EPQ模式

基本假設：

a.每年需求及持有成本、設置成本是可估計的

b.無安全存貨之考量，生產率與需求率為一定值，當物料用完時即開

   始生產運作。

c.允許缺貨補貨

d.沒有數量折扣

符號說明：

T：計劃週期數

R：年需求數量

q：每週期訂購數量

a：每週其每單位支持有成本

b：每週期每單位之缺貨成本

c：每週期訂購成本

s：最大存貨數量

d：需求率

p：生產率

　

總成本函數 = 設置成本 + 持有成本 + 缺貨成本

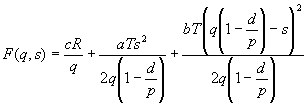
則           令其0，

得到     

          

　

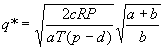
模糊化EPQ模式：

由此我們可以得到傳統EPQ模式之p^*及s^* ，但是此方式無法處理其生產批量的不確定性，故我們考慮模糊的生產數量  及最大存貨數量 ，再由模糊三角函數可找出模糊的生產數量 之隸屬函數：

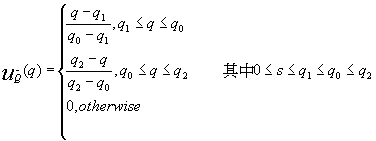
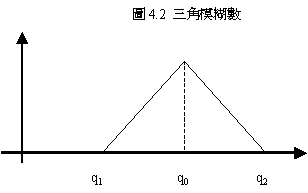
經由質中心函數可解模糊化： 

 

　

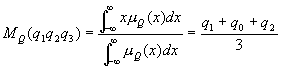
總成本：

            ,    

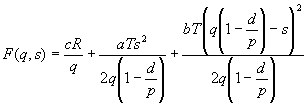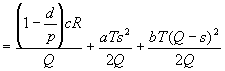                      其中  ph=Q

令F ( Q , s )=y>0

             

解Q值

   

   

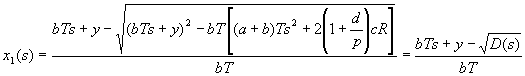
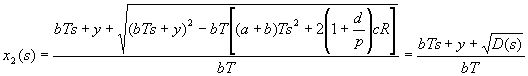
其中 

再令 

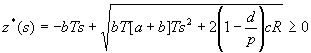
可得到：

                        if  ,  then ,

                        if  ,  then  , 

由擴展定理我們可以獲得 知隸屬函數如下：

                                                   

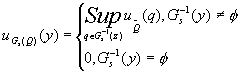
因此我們得到：

                                     

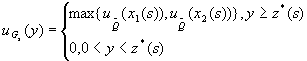
最佳生產批量及總成本

  令

     

    

   

    

                                    

                             其中

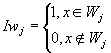
為了使  M(q₁*,q₀*,q₂*,s*) 為最小，我們利用Nelder-Mead method可找出 q₁*,q₀*,q₂*and s^*使得 M(q₁*,q₀*,q₂*,s*) 為極小值，故我們利用

q₁^{為R(1),X(1),W(1),E(1)，其中R(1)<X(1)<W(1)<E(1)}

q₀^{為R(2),X(2),W(2),E(2)，其中R(2)<X(2)<W(2)<E(2)}

q₂^{為R(3),X(3),W(3),E(3)，其中R(3)<X(3)<W(3)<E(3)}

 s ^{為R(4),X(4),W(4),E(4)，其中R(4)<X(4)<W(4)<E(4)}

我們發現若出 q₁*,q₀*,q₂*and s^*，使的得M(q₁*,q₀*,q₂*,s*) 為局部極小值，則

                                    q**=(q₁+q₀+q₂)/3

是模糊觀念下的經濟生產批量，s*則是最佳存貨數量，而 M(q₁*,q₀*,q₂*,s*) 則是模糊觀念下的最佳總成本。

　

回首頁