二、模糊理論

        在現實生活中許多對於事物的描述都是模糊不清的，像是「天氣很熱」、「距離很遠」等。因為每個人對於外在環境的感受不同，對於同一件事情會有不同程度的感受，而再表達這些感受時通常都是相當模糊的。為了要將日常生活中實際存在的模糊敘述與模糊現象加以分析，以期望能得到較確切的表達，來作為科技上的控制或是管理時的決策分析及其他領域的應用，模糊理論的研究分析方法已被廣泛的運用。

2.1模糊集合

         傳統的明確集合是屬於二元的，論域中的元素對某一集合的關係只有兩種，也就是”包含”與”不包含”。但是在日常生活中，我們對事物的描述方式，大都具有模糊性，而不是可以非常明確的分為兩類的。

       模糊集合沒有明確的邊界，元素對集合的關係不再是二元的，而是以依照其類似的程度而給予其歸屬程度值。我們可以定義在論域U中的一個模糊集合A為：

   A＝｛（x，μA (x)）∣xμA∪B(x) = s[μA (x)，μB (x)]U｝

其中，μA(˙)是模糊集合A的歸屬函數，μA（x）代表元素x對模糊集合A的歸屬程度。歸屬函數μA(˙)將論域U映射至歸屬空間M中。當M=｛0，1｝時，集合A不再是模糊集合，也就是說：模糊集合A退化為明確集合A，而歸屬函數μA（x）退化為特徵函數 。一般說來我們將模糊集合的歸屬空間M設定為【0，1】。值得一提的是，任何函數值是位於0與1之間的函數都可以成為歸屬函數，但是，要能夠符合常理才行。

   以下介紹模糊集合的另一種表示法：

對於離散的論域來說U＝｛x₁，x₂，…x_N｝，此模糊集合可以表示如下：

    A＝｛(x₁，μ_A (x₁))，(x₂，μ_A (x₂))，…，(x _N，μ_A (x _N))｝

   另一種表示法為：

   A＝μ₁ /x₁＋μ₂ /x₂＋…＋μ_N /x_N =μ_A (x)

其中”＋”代表”聯集”，μ_A (x)為元素對此模糊集合的歸屬程度。

注意在此種表示法中，我們只考慮具有非零歸屬函數值的元素。

若論域為連續的，則我們可以用以下的表示法來表示模糊集合：

   A＝μ_A (x)

2.2 歸屬函數

       只要是函數都是位於【0,1】的區間內的函數，都可成為歸屬函數，以上介紹一些常見的歸屬函數：

S-函數：

因其圖形長的像S所以稱為S-函數。當x = m時，S (m; l, m, n) = 0.5，所以m點稱為交越點(Crossover Point)。通常可用S-函數來表示「x是大的」這樣的模糊概念。

　

S(x;l,m,n) =	0,                           x≦l
	2[(x-l)/(n-l)]2,         l≦x≦m
	1-2[(x-l)/(n-l)]2,      b≦x≦n
	1,                            x≧n

Z-函數：

Z-函數為S-函數的補集。以S=0.5為基準，將S-函數上下顛倒即可得到Z-函數的圖形。

Z (m; l, m, n) = 1 - S (m; l, m, n)

通常可用Z-函數來表示「x是小的」這樣的模糊概念。

π-函數：

π-函數的圖形有如倒置的鍾，故又有「倒鍾形函數」之稱。

其中參數b稱為π-函數的帶寬(Bandwidth)。π-函數常用以表達「x 大約是 c」這樣的模糊概念。

指數函數：

指數函數又稱高斯分布函數。形狀有點類似π-函數，只是所涵蓋範圍延伸至正負無限大處。一般以兩個參數即可完全描述出指數函數的特性：

        N (x; m, σ) = exp [ -(x-m)²/σ²]

m表示指數函數的中心點，而σ則描述函數延伸(Spread)的程度。指數函數常被利用於適應性的(Adaptive) Fuzzy控制系統中。

2.3模糊運算

   接下來我們介紹一些常用的模糊集合之運算子，令A與B為定義於論域U之模糊集合，則：

1. 補集：當歸屬function值介於0與1之間時，模糊集合A的補集A’定義為：

   ，

  μ_A ≡ 1-μ_A(x) ，

2.交集：模糊集合A與B的交集之符號為A∩B，定義為：

   ，

   其中” ”代表”取小運算子（min）”，因此可知：

   A∩B A以及A∩B B

3.聯集：模糊集合A與B的交集之符號為A∪B，定義為：

   ，

   其中” ”代表”取小運算子（min）”，因此可知：

   A∪B A以及A∪B B

4.相等：模糊集合A與B為相等的充要條件為：

   ＝ ，

   而兩個模糊集合的”相似程度”的量測可用：

   E（A，B）

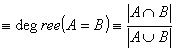
其中”∩”代表交集，” ∪”代表聯集，當A＝B時，E（A，B）＝1，當 ＝0時，也就是說A與B完全不重疊時，E（A，B）＝0。

5.子集：模糊集合A與B的子集的充要條件為：

   ≦ ，

而模糊集合B對模糊集合A的”包含程度”的量測可用：

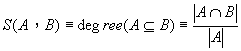
我們將其它同時適用於模糊集合與傳統的明確集合所常用的定理整理於下的表格中。但須注意在模糊集合中，傳統的集合論中的”排中律”（E∪E’＝U）”與”矛盾律（E∩E’＝Φ）”是不成立的，也就是說，對模糊集合A而言：

   A∪A’≠U以及A∩A’ ≠Φ

    前述之運算子是模糊集合最常使用的型式，但實際上從明確集合運算延伸至模糊集合運算的方法並非只有這一種方式，還有許多符合應有的集合運算特性的%運算子，都己陸續被發表過。

模糊集合運算子之性質

回首頁