![]() 五、與傳統EPQ之比較
五、與傳統EPQ之比較
傳統之EPQ模式:
總成本 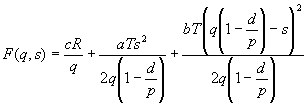
生產批量
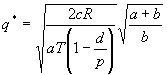
模糊化後之EPQ模式:
生產批量 q**=(q1+q0+q2)/3
總成本
![]()
其中 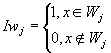
![]()
![]()
![]()
![]()
在可缺貨補貨的EPQ模式下,生產批量模糊化之生產批量q**,及總成本M與傳統EPQ模式的差異如下。
令 每週每單位之持有成本 a = 10
每週每單位之缺貨成本 b = 20
年需求量 R =2000
計劃週期數 T =12
生產率 p =200
需求率 d = 166.67
傳統EPQ模式可以得到:
q* = 244.95
s* = 27.22
F ( q* , s* ) =3265.99
模糊化後之EPQ模式可得到結果如表5.1:
表5.1 模糊化EPQ模式相關表
rq:生產批量敏感性
rc:總成本敏感性
|
|
q1,q0,q2
很靠近q* |
q1,q0,q2
遠大於q* |
q1,q0,q2
遠小於q* |
|
S=s* |
q**
= 248.48 M
= 3267.05 rq
= 1.44% rc
= 0.03% |
q**
= 326.38 M
= 3673.73 rq
= 33.25% rc
= 12.48% |
q**
= 204.60 M
= 3425.78 rq
= -16.44% rc
= 4.89% |
|
S很靠近s* |
q**
= 250.93 M
= 3268.91 rq
= 2.44% rc
= 0.06% |
q**
= 313.85 M
= 3569.01 rq
= 28.13% rc
= 9.28% |
q**
= 214.24 M
= 3357.78 rq
= -12.54% rc
= 2.80% |
|
S遠小於s* |
q**
= 250.93 M
= 3316.43 rq
= 2.44% rc
= 1.54% |
q**
= 306.15 M
= 3946.37 rq
= 24.98% rc
= 20.83% |
q**
= 202.56 M
= 3350.77 rq
= -17.31% rc
= 2.60% |
|
S遠大於s* |
q**
= 242.64 M
= 3541.51 rq
= -0.92% rc
= 8.44% |
q**
= 300.14 M
= 3339.40 rq
= 22.53% rc
= 2.25% |
q**
= 201.74 M
= 4076.67 rq
= -17.64% rc
= 24.82% |
由於 M(q1*,q0*,q2*,s*) 有四個變數,我們無法使用一般之方法解出最佳解,因此,數值分析法Nelder-Mead Algorithm的方法,找出近似的最佳解 q1*,q0*,q2*,s*,再由q1*,q0*,q2*,s*解出最佳生產批量及最小總成本,而由該演算法可得知需假設五組初值去處理該演算法。
由表5.1,我們可以得知(q1,q0,q2 很靠近q*,S=s*)所得到的解為
q** =
248.48、M = 3267.05、rq
= 1.44%、
所以在此模糊理論下的總成本是:
M(q1*,q0*,q2*,s*) = 3267.05
最佳生產批量是:
q** = 248.48
在此情形下,模糊理論EPQ的總成本會稍微高於傳統EPQ的總成本約0.03%,而模糊生產批量則略高於傳統生產批量約1.44%。
當S = s*時我們可以看出q**由 204.60 增加至 326.38 時,總成本先由高轉低,當q** = 248.48 可使總成本最低,當q** = 326.38 時總成本又增加了,如圖5.1:
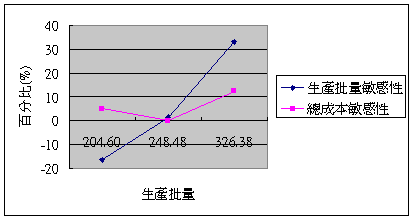
圖5.1 當S = s*時訂購數量與總成本之變化
而再其他的十一種情況下所得的解皆不是最佳解,故我們知道在決定q1,q0,q2,s之初值時,以最接近q*,及S = s*所得到的解較能夠接近最佳近似解。